Simple Cyclic Hamming (15,11,3) FEC
This post is the implementation part of the my post on simple cyclic Hamming code where I did some math workout on this type of forward error-correction code (FEC). I am doing it for fun since I think it is simple enough to implement it in FPGA. The generator for this exercise is \(g(x)=1+x+x4\) for an \((n,k,d) \equiv (15,11,3)\) code.
Implementation
If the data to be encoded is parallel data block, the encoded message can simply be done with simple combinational logic based on the \(G\) matrix, likewise for the decoder logic, but this is too boring. I choose to complicate this matter by assuming that the input data bits to be encoded or decoded arrive serially, perhaps from a transceiver part of the circuit. This way I can implement it with divider circuit and get myself frustrated with timing closure and everything else. Simple and elegant way is not always paid off. This is what I am going to do.
For this exercise, I am targeting the Xilinx Artix FPGA device. I create three verilog modules,
. Encoder for encoding 11-bit message to 15-bit message.
. Decoder for decoding the 15-bit receiving message.
. Corrector is for correcting the error if syndrome indicates the error.
The encoder
The encoder takes a stream of 11-bit input message and encodes it to 15-bit messages in systematic form. The input bit is clocked in bit-by-bit to the encoder whenever enc_enable is asserted. On the completion of the encoding process, the rdy is asserted as an output ready indicator so that the 15-bit encoded message can be read.
Th encoder part of this module is between line 16-46. The divider circuit that forms the \(P_i\) bits is between line 49-67. The lines that forms the output coded word are at line 29 and 32. The sample simulation below shows one of the encoded message. Any \(2^{11}\) input message words can be encoded by this circuit and matches with the multiplication of the \(G\) matrix. This is how I know that the divider circuit works.
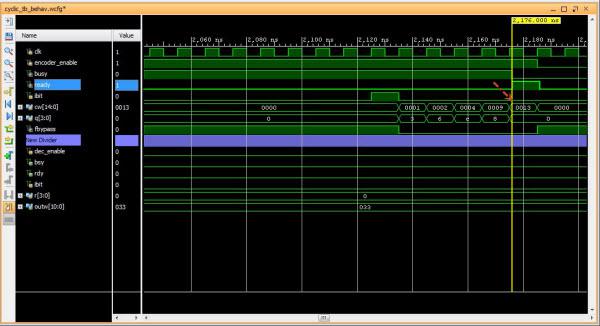
Fig1: encoded message 01h
The decoder and FEC
The FEC decoder is the reverse of the encoder where it takes in the serial 15-bit code word, computes the syndrome and if any 1-bit error is detected, the instantiated lookup bit correction will return the correctable bit position. This completed the FEC process.
The divider circuit (line 44-65) for the decoder is similar to that of the encoder, but it performs syndrome computation by taking all the input bits having the remainder shifted into the decoded output word. If the remainder is non-zero, it set ierr bit as an enabler for lookup11 module (line 67-73). The table lookup module returns the corresponding bit error, bit_correction, where it does the modulo-2 sum to the decoded word (line 16). This is the FEC.
The lookup module is a simple ROM type lookup table using the 4-bit syndrome as the index to the correction bit. It returns non-zeros for errbits on any error, zeros otherwise. It covers both message bits and parity bits.
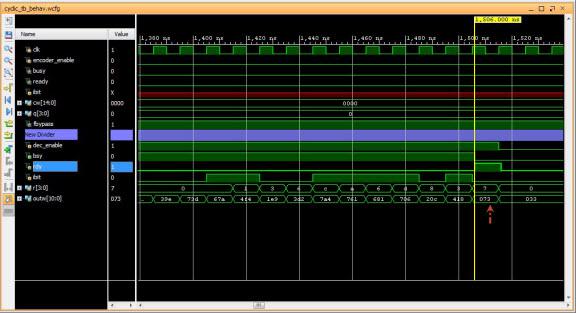
Fig1: decoded non-error message 0x73d for 0x73
I test the FEC logic with random test vector for several coded words out of \(2^{11}\) possible coded words and I can verify that any single bit error is corrected as it is a \(t=1\) FEC. The code rate for this implentation is \(\frac{k}{n} = \frac{11}{15}\)
What is really needed for this FEC is only to correct the message error bit, any bit of the 11-bit. The err bit can be used as a request for retransmission if the error bit falls into the parity area. This means that certain syndrome in the look up table will be partially used.
Shortened code \((n-l,k-l,d)=(12,8,3)\) can also be obtained using this exact scheme with minimal change to the logic because it is more practical to do it in 8-bit rather than 11-bit. It is no longer cyclic, but it offers the same error-correcting capability as its normal version.
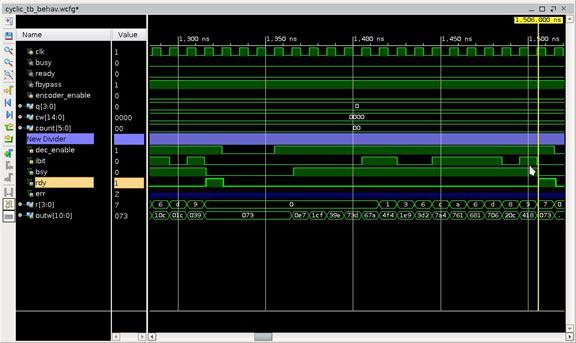
Fig1: FEC 1-bit error (bit 6) in coded word. Decoded and Corrected 0x33d for 0x73
I believe that my implementation is what is called Meggitt decoder. Since I do not take into account the error confinement, it has certain restriction such as error trapping so future improvement is needed.
Conclusion
Cyclic code FEC of this type can be easily implemented with shift registers to perform modulo division. The FEC in this exercise may not be efficient, but if it requires that the FEC be implemented with minimal gates then it would be practical.
When time permits, I will try to implement \(t > 1\) FEC.